Бета-коэффициент: для чего нужен и как его рассчитать

При оценке компании доходным методом, то есть путем дисконтирования будущих денежных потоков, очевидно значимым моментом является определение ставки дисконтирования, с помощью которой эти самые будущие денежные потоки будут приводиться к текущей стоимости.

Не вдаваясь в подробности расчета дисконтированных денежных потоков, скажу, что базово потоки делятся на два вида: денежные потоки на собственный капитал и денежные потоки на инвестированный капитал (собственный капитал + заемное финансирование). Отличаются и ставки дисконтирования для двух разновидностей потоков. Поскольку речь далее пойдет про смысл и методику расчета коэффициента бета, то обратимся к ставке дисконтирования для собственного капитала. Она, к слову, нужна и для расчета ставки дисконтирования для капитала инвестированного.

В современной практике для расчета ставки дисконтирования денежный потоков на собственный капитал в большинстве случаев применяется модель CAPM (Capital Asset Pricing Model), что в дословном переводе означает «модель ценообразования капитальных активов».

Концепция CAPM была разработана на основе портфельной теории Г. Марковица, наиболее применимая на сегодняшний день интерпретация данной концепции принадлежит У. Шарпу, поэтому она зачастую называется его именем. Ставка доходности, рассчитанная по модели CAPM, определяет, какой должна быть доходность актива, добавляемого к портфелю, с учетом его рыночного риска. Поскольку именно требуемой доходностью определяется ставка дисконтирования будущих денежных потоков, рассчитанная по описываемой модели доходность может использоваться в качестве такой ставки. Рассчитанная по модели CAPM требуемая норма доходности в отношении актива является, таким образом, общей для рынка, то есть лишена субъективной составляющей.

Ниже приведена формула расчета доходности по CAPM:

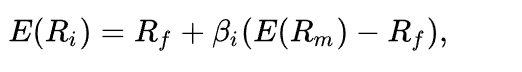
Где:

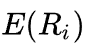Ожидаемая ставка доходности актива.

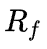Безрисковая ставка доходности (как правило, ОФЗ).

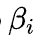Бета-коэффициент, мера рыночного риска актива.

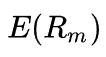Ожидаемая доходность рыночного портфеля (для простоты расчета чаще всего берется доходность индекса).

Выражение в скобках представляет собой премию за риск для определенного рынка (рынка, для которого мы берем рыночную доходность и безрисковую ставку). Бета-коэффициент, таким образом, выступает мерой рыночного риска: он определяет, в какой степени конкретный актив подвержен рыночному риску, то есть как соотносится изменение доходности актива с изменением доходности рыночного портфеля.

Поскольку доходность актива в случае с акциями определяется движением котировок, коэффициент бета также часто интерпретируют как волатильность: чем выше коэффициент – тем волатильнее акция, для которой он рассчитан. Волатильность же измеряется в данном случае относительно рыночного портфеля.

Расчет бета-коэффициента:

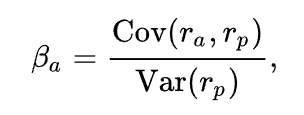
Где:

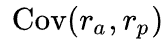Ковариация доходностей актива, для которого рассчитывается коэффициент бета с доходностью рыночного портфеля (эталона).

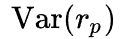Дисперсия доходности рыночного портфеля.

Коэффициент бета, таким образом, может принимать любое значение, однако чаще всего находится в диапазоне от -1 до 1, или, еще чаще, в диапазоне от 0 до 1. Ниже приведена интерпретация основных интервалов значений.

• Бета 0. Такое значение коэффициента означает, что доходность актива не изменяется вовсе, то есть он является безрисковым. Если подставить такое значение в первую формулу, мы получим доходность, равную безрисковой ставке.

• Бета в диапазоне от 0 до 1. Такое значение коэффициента означает, что доходность актива и рыночного портфеля изменяются сонаправленно, однако изменение доходности актива (волатильность) ниже, чем у рыночного портфеля.

• Бета равна 1. Означает, что доходности актива и рыночного портфеля меняются одинаково, то есть корреляция 100%.

• Бета коэффициент больше 1. Означает, что доходность актива и рыночного портфеля меняются сонаправленно, однако изменчивость доходности актива выше, нежели рыночного портфеля. То есть, выше его риск.

• Бета в диапазоне от -1 до 0. Выводы аналогичны диапазону от 0 до 1, однако движение доходностей является противоположным.

• Бета равна -1. Означает, что доходности актива и рыночного портфеля изменяются в одинаковой мере, но разнонаправленно.

• Бета меньше -1. Выводы аналогичны значению больше 1, однако движение доходностей разнонаправленное.

Поскольку, как сказано выше, доходность определяется движением котировок, под изменением доходности следует понимать изменение котировок.

Как рассчитать бета-коэффициент?

Поскольку расчет бета-коэффициента – достаточно трудоемкое занятие, сегодня это проще всего сделать с помощью Excel. В таблице ниже для примера взяты данные по торгам с 1 ноября 2021 года, однако на практике лучше использовать более длительный период, хотя бы от 100 торговых дней.

Для каждого периода рассчитываем доходности Ra (доходность акции) и Rp (доходность портфеля).

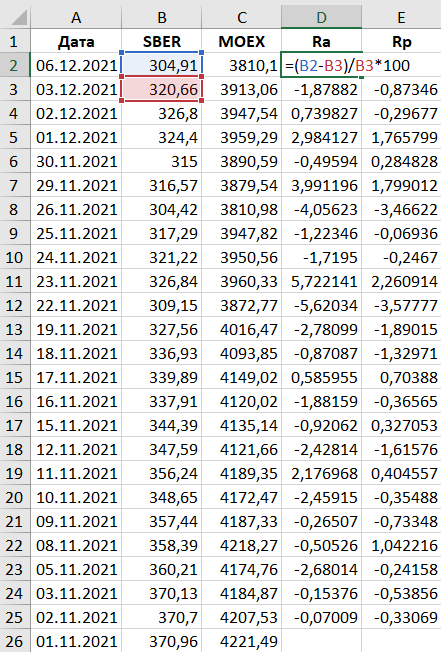
Далее есть два способа рассчитать бета-коэффициент.

Способ №1

Для расчета коэффициента будем использовать формулы Excel «ИНДЕКС» и «ЛИНЕЙН», в значениях из таблицы выше формула примет вид:

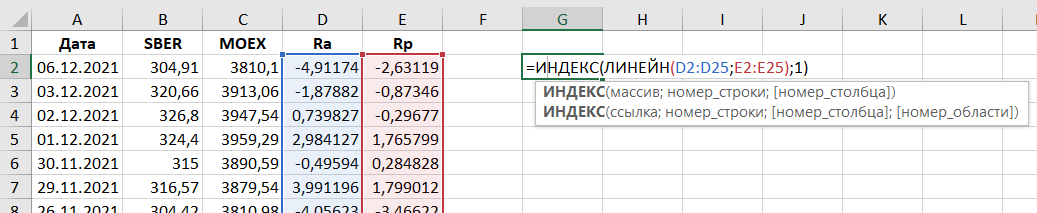
Получаем значение бета-коэффициента, равное 1,56, что в соответствии с описанной выше интерпретацией говорит нам о том, что на данном временном промежутке акции Сбера были более волатильными, чем рыночный портфель, в качестве которого использовался индекс Московской биржи.

Способ №2

На зависимость между доходностями акции и рыночного портфеля можно смотреть как на линейную регрессию.

Уравнение простой (парной) линейной регрессии имеет следующий общий вид:

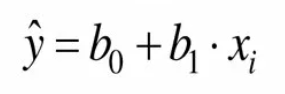
Коэффициент b1 и определяет тесноту связи переменных. Он и будет бета-коэффициентом в случае построения парной линейной регрессии для наших значений доходностей. Чтобы построить регрессию в Excel потребуется подключить в настройках пакет анализа данных.

На вкладке «Файл» необходимо найти раздел «Параметры».

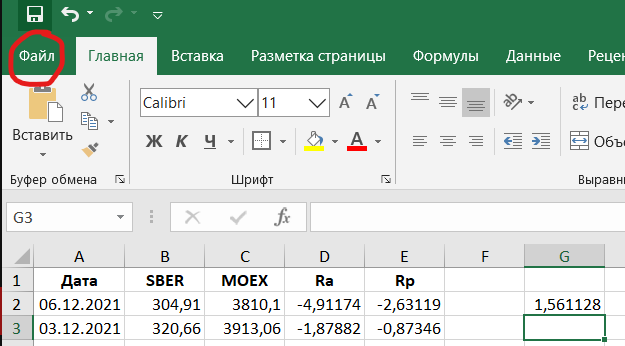
Он находится в левом нижнем углу.

В появившемся окне переходим в раздел «Настройки» и нажимаем последовательно как на картинке:

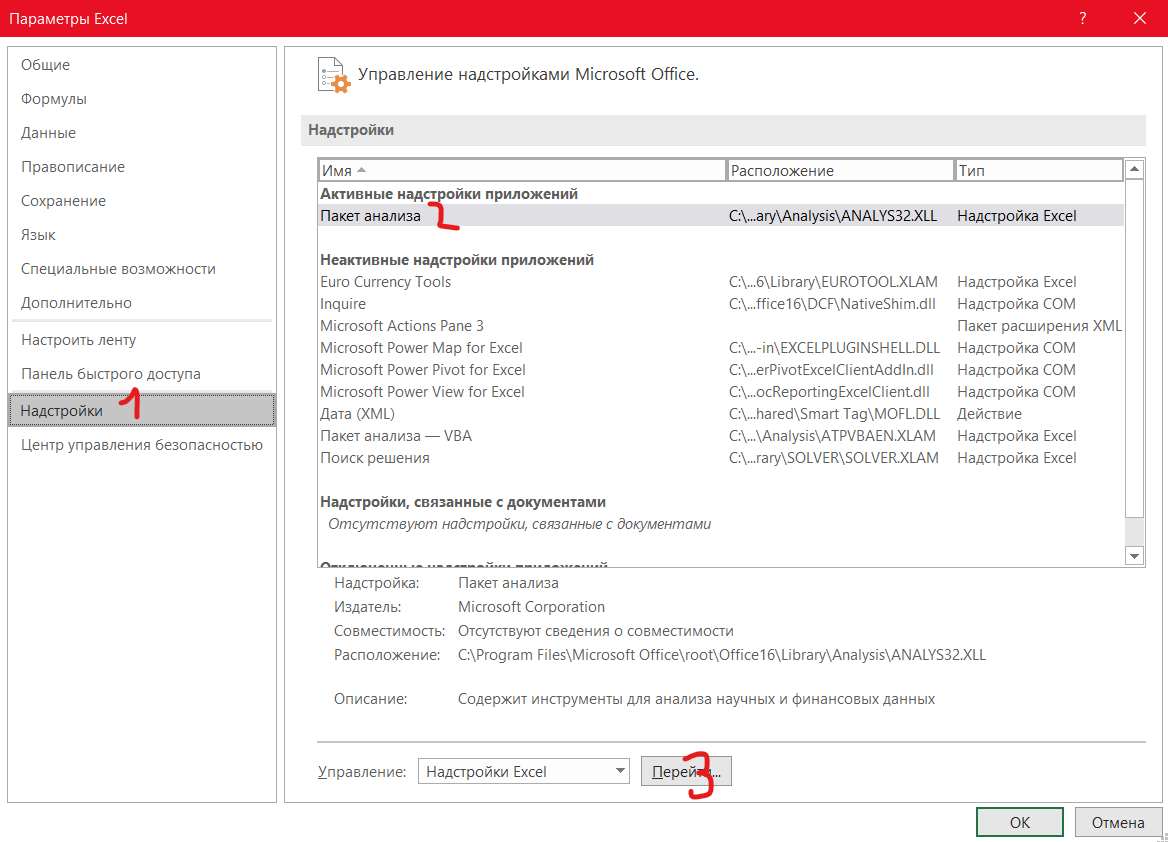
В появившемся окне ставим галочку в поле «Пакет анализа».

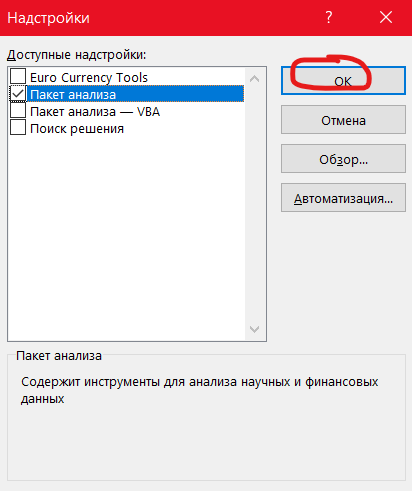
Теперь пакет анализа включен и найти его можно на вкладке «Данные» в правом верхнем углу.

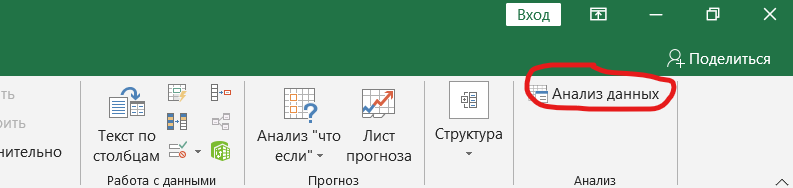
Далее дело за малым. Нажимаем на «Анализ данных». Выбираем в списке «Регрессия».

Заполняем входные диапазоны: Y – это значения доходностей акции, X – значения доходностей индекса (рыночного портфеля). Ставим галочку в разделе «Параметры вывода» в графе «Новый рабочий лист», нажимаем «Ок».

Открывается новый рабочий лист, на котором мы видим множество различных параметров нашей регрессии. Нас же интересует бета-коэффициент, который выделен желтым цветом.

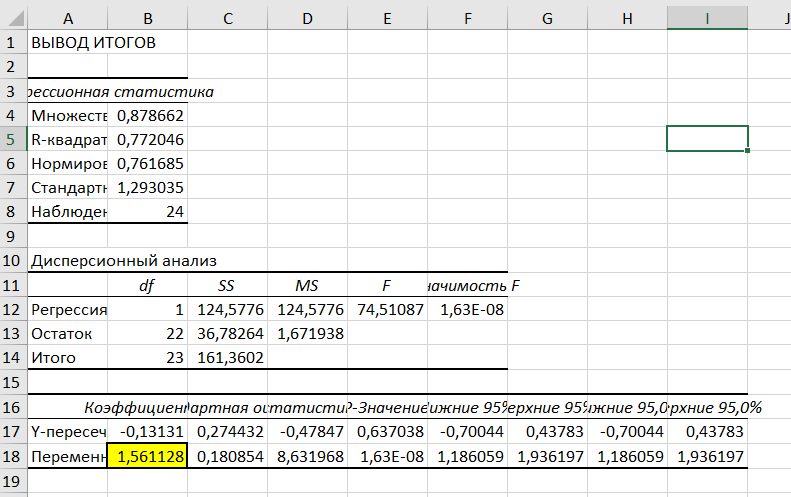
В целом способы по своей сути одинаковые, просто во втором случае мы получаем дополнительные данные, которые будут интересны разве что тем, что хорошо разбирается в статистике. Приведенные данные позволяют оценить достоверность выявленной зависимости, статистическую значимость результата.

Бета-коэффициент можно считать для различных периодов, в зависимости от того, насколько сильно в представлении считающего менялся характер связи между акцией и индексом. Так, чем стабильнее и рынок и чем он более развит – тем больше может быть период для расчета коэффициента.

Если деятельность компании претерпела серьезные изменения, которые позволяют предположить, что степень влияния на ее деятельность рыночных рисков изменилась, не стоит принимать к расчету большой период до соответствующих изменений, так как такие значения могут исказить результат и «перевесить» более поздние и актуальные значения при расчете.